Math Homework #7 Solutions

Problem 1. Prove each of the following (using properties of integers and the relevant
definitions from class concerning rational numbers):
(a) Addition of rational numbers is well-defined.
(b) Addition of rational numbers is commutative.
(c) The distributive law holds for rational numbers.

Solution. Note that in what follows, whenever I write a rational number 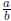or
an ordered pair (a, b), I assume automatically that a ∈ Z and b ∈ .

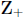(a) Suppose that (a, b) ~ (a', b') and (c, d) ~ (c', d'). That is, ab' = a'b and
cd' = c'd. Then according to our definitions, we have

(a, b) + (c, d) = (ad + bc, bd) and (a', b') + (c', d') = (a'd' + b'c', b'd').

Comparing the results, we find

(ad + bc)(b'd') - (a'd' + b'c')(bd)
= (adb'd' - a'd'bd) + (bcb'd' - b'c'bd)
= dd'(ab' - a'b) + bb'(cd' - c'd)
= dd' · 0 + bb' · 0 = 0,

since ab' = a'b and cd' = c'd. I conclude that

(a, b) + (c, d) ~ (a', b') + (c', d').

Hence addition respects the equivalence relation ~, and addition of rational
numbers is well-defined.

(b) Given rational numbers 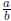and 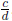, I have



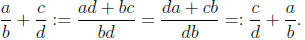
This proves that addition of rational numbers is commutative.

(c) Given rational numbers 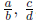, and 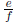, I have on the one hand that



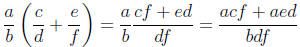
and on the other hand that



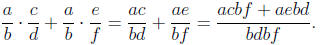
To verify that the results are the same, I cross-multiply and check

(acf + aed)(bdbf) - (acbf + aebd)(bdf) = ab²df((cf + ed) - (cf + ed)) = 0.

So multiplication of rational numbers is distributive over addition.

Problem 2. The wrong way to add fractions. Given rational numbers and , suppose we
define a 'new' kind of sum



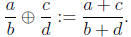
(a) While it's appealingly simple, this definition of 'addition' has the slight drawback
that it gives answers that are inconsistent with our expectations (e.g.
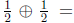
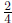?). However, all expectations aside, this definition has a worse flaw: it isn't even
consistent with itself. Give an example to illustrate.

(b) On the other hand, the above idea for adding rational numbers isn't entirely without
merit (this is a major understatement—if you ask me about it, I'll explain). Show
that if 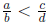, then 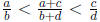. (I should point out that this is another way to see
that Q has the density property.)

Solution.

(a) Note, for instance,



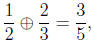
whereas



However, 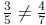. Hence ⊕ can't be a genuine operation on rational numbers,
because it depends on how the numbers are expressed, rather than
just on the numbers themselves.

(b) First I show that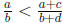

a(b + d) - (a + c)b = ad - bc < 0|

because .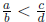

Similarly, to see that 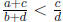, I cross-multiply and check

(a + c)d - c(b + d) = ad - bc < 0

Problem 3. Show that 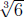is irrational. That is, there is no x ∈ Q such that x³ = 6. Of
course, you want to imitate the proof that 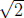is irrational. But be careful: 6 is not prime.

Solution.

Proof. Suppose (in order to get a contradiction) that there exists x ∈ Q such
that x³ = 6. Then I can write x = p/q, where p, q ∈ Z satisfy q > 0 and
gcd(p, q) = 1. Since x³ = 6, I infer p³ = 6q³. Since 2|6 and 6|p³, it follows
that 2|p³. Since 2 is prime, it further follows that 2|p. Now I write p = 2k
for some k ∈ Z. The equation p³ = 6q³ becomes 2³k³ = 6q³, or a little more
simply 2²k³ = 3q³. In particular, 2|3q³. Since 2 is prime and does not divide
3, I infer that 2|q³ and therefore 2|q. But since I already showed that 2|p, this
contradicts the assumption that p and q are relatively prime. I conclude that
there is no x ∈ Q satisfying x³ = 6.

Problem 4. Let n ≥ 2 and m ≥ 0 be integers. Show that 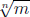is rational if and only if
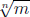
is an integer. More precisely, show that

if x ∈ Q satisfies xⁿ = m, then x is actually an integer.

Hint: There are a couple of different ways to do this, each resembling (but not perfectly)
the proof that is irrational. Note that a rational number x = a/b given in lowest terms is
an integer if and only if b ≥ 2. It might help to think first about the case where b is prime.

Solution.

Proof. Suppose that xⁿ = m for some x ∈ Q. I can write x = for some
integers a, b such that gcd(a, b) = 1. Suppose to get a contradiction that x
is not an integer. Then b ≥ 2 and must have a prime factor: b = pk for
some prime number p and integer k. Substituting x = a/pk into the equation
xⁿ = m, I obtain

aⁿ = mpⁿkⁿ.

In particular, p|aⁿ which, since p is prime, means that p|a. This contradicts
the fact that a and b have no common factors larger than 1. Hence x must be
an integer after all.