A Math Primer
Algebraic Expressions
Variables
Letters represent an unknown or generic real
number
Sometimes with restrictions, such as a member
of a certain set, or the set of values that makes an
equation true.
Often a letter from the end of the alphabet: x, y, z
Or a letter that stands for a physical quantity: d
for distance, t for time, etc.
Constants
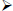Fixed values, like 2 or 7
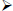Can also be represented by letters: a, b, c, p, e, k
Terms
Terms are Separated by + or –
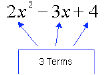
Factors
Factors are multiplied together.
Coefficients
Coefficients are constant factors that multiply a
variable or powers of a variable
The middle term has 2 factors, –3 and x. We say that
the coefficient of x is –3.
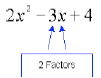
The first term has three factors, 2 and two factors of
x. We say that 2 is the coefficient of x2.
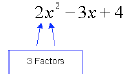
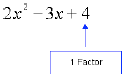
The last term is a factor all by itself (although the
number 4 could be factored into 2 x 2).
Simplifying Algebraic Expressions
By “simplifying” an algebraic expression, we mean
writing it in the most compact or efficient manner,
without changing the value of the expression. This
mainly involves collecting like terms, which means
that we add together anything that can be added
together. The rule here is that only like terms can be
added together.
Like (or similar) terms
Like terms are those terms which contain the same
powers of same variables. They can have different
coefficients, but that is the only difference.
Examples:
3x, x, and –2x are like terms.
2x2, –5x2, and are like terms.
xy2, 3y2 x, and 3xy2 are like terms.
xy2 and x2 y are NOT like terms, because the same
variable is not raised to the same power.
Combining Like terms
Combining like terms is permitted because of the
distributive law. For example,
3x2 + 5x2 = (3 + 5)x2 = 8x2
What happened here is that the distributive law was
used in reverse—we “undistributed” a common
factor of x2 from each term. The way to think about
this operation is that if you have three x-squareds,
and then you get five more x-squareds, you will then
have eight x-squareds.
Example: x2 + 2x + 3x2 + 2 + 4x + 7
Starting with the highest power of x, we see that
there are four x-squareds in all (1x2 + 3x2). Then we
collect the first powers of x, and see that there are six
of them (2x + 4x). The only thing left is the constants
2 + 7 = 9. Putting this all together we get
x2 + 2x + 3x2 + 2 + 4x + 7
=
4x2 + 6x + 9
Parentheses
∞ Parentheses must be multiplied out before
collecting like terms
You cannot combine things in parentheses (or other
grouping symbols) with things outside the
parentheses. Think of parentheses as opaque—the
stuff inside the parentheses can’t “see” the stuff
outside the parentheses. If there is some factor
multiplying the parentheses, then the only way to get
rid of the parentheses is to multiply using the
distributive law.
Example:
3x + 2(x – 4) = 3x + 2x – 8
= 5x – 8
Minus Signs: Subtraction and Negatives
Subtraction can be replaced by adding the opposite
3x – 2 = 3x + (–2)
Negative signs in front of parentheses
A special case is when a minus sign appears in front
of parentheses. At first glance, it looks as though
there is no factor multiplying the parentheses, and
you may be tempted to just remove the parentheses.
What you need to remember is that the minus sign
indicating subtraction should always be thought of as
adding the opposite. This means that you want to add
the opposite of the entire thing inside the
parentheses, and so you have to change the sign of
each term in the parentheses. Another way of looking
at it is to imagine an implied factor of one in front of
the parentheses. Then the minus sign makes that
factor into a negative one, which can be multiplied
by the distributive law:
3x – (2 – x)
= 3x + (–1)[2 + (–x)]
= 3x + (–1)(2) + (–1)(–x)
= 3x – 2 + x
= 4x – 2
However, if there is only a plus sign in front of the
parentheses, then you can simply erase the
parentheses:
3x + (2 – x)
= 3x + 2 – x
A comment about subtraction and minus signs
Although you can always explicitly replace
subtraction with adding the opposite, as in this
previous example, it is often tedious and
inconvenient to do so. Once you get used to thinking
that way, it is no longer necessary to actually write it
that way. It is helpful to always think of minus signs
as being “stuck” to the term directly to their right.
That way, as you rearrange terms, collect like terms,
and clear parentheses, the “adding the opposite”
business will be taken care of because the minus
signs will go with whatever was to their right. If what
is immediately to the right of a minus sign happens
to be a parenthesis, and then the minus sign attacks
every term inside the parentheses.
Solutions of Algebraic Equations
Up until now, we have just been talking about
manipulating algebraic expressions. Now it is time to
talk about equations. An expression is just a
statement like
2x + 3
This expression might be equal to any number,
depending on the choice of x. For example, if x = 3
then the value of this expression is 9. But if we are
writing an equation, then we are making a statement
about its value. We might say
2x + 3 = 7
A mathematical equation is either true or false. This
equation, 2x + 3 = 7, might be true or it might be
false; it depends on the value chosen for x. We call
such equations conditional, because their truth
depends on choosing the correct value for x. If I
choose x = 3, then the equation is clearly false
because 2(3) + 3 = 9, not 7. In fact, it is only true if I
choose x = 2. Any other value for x produces a false
equation. We say that x = 2 is the solution of this
equation.
Solutions
The solution of an equation is the value(s) of the
variable(s) that make the equation a true
statement.
An equation like 2x + 3 = 7 is a simple type called a
linear equation in one variable. These will always
have one solution, no solutions, or an infinite number
of solutions. There are other types of equations,
however, that can have several solutions. For
example, the equation
x2 = 9
is satisfied by both 3 and –3, and so it has two
solutions.
One Solution
This is the normal case, as in our example where the
equation 2x + 3 = 7 had exactly one solution, namely
x = 2. The other two cases, no solution and an infinite
number of solutions, are the oddball cases that you
don’t expect to run into very often. Nevertheless, it is
important to know that they can happen in case you
do encounter one of these situations.
Infinite Number of Solutions
Consider the equation
x = x
This equation is obviously true for every possible
value of x. This is, of course, a ridiculously simple
example, but it makes the point. Equations that have
this property are called identities. Some examples of
identities would be
2x = x + x
3 = 3
(x – 2)(x + 2) = x2 – 4
All of these equations are true for any value of x.
The second example, 3 = 3, is interesting because it
does not even contain an x, so obviously its
truthfulness cannot depend on the value of x! When
you are attempting to solve an equation algebraically
and you end up with an obvious identity (like 3 = 3),
then you know that the original equation must also be
an identity, and therefore it has an infinite number of
solutions.