Adding and subtracting polynomials

Like terms:

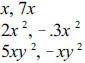
Unlike terms:

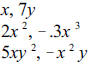
Ex. 1
Simplify by combining like terms:
1.

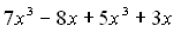
It may be helpful to rewrite the problem putting your like
terms together: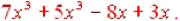 . When you
combine like terms, add/subtract the coefficients only:
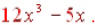. This is the final answer because that can’t be
simplified any more.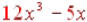  and
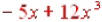
represent the same expression but the first one is in
descending order. This is the acceptable way to write a
polynomial. That means the term with the highest power
goes first and the powers descend from there.

Ex. 2
Add:
1.

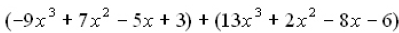
This is an example of
addition of two polynomials.
There are two methods that
you can use to add these:
horizontal format or vertical
format.

With the horizontal format, we’ll basically do what we did in example 1. We’ll rewrite
the problem putting the like terms together:
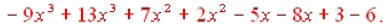Now combining like terms gives us
our answer: 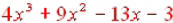. When using the vertical format, we’ll line the like
terms up in a column and add the coefficients: .

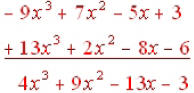In the next example we’ll subtract polynomials but first let’s revisit the definition of subtraction.
Subtraction means to add the opposite. So 3 - 5 is the same as 3 + - 5.

Ex. 3
Subtract:
1.

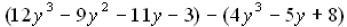
If subtraction means to add the
opposite, then I’ll rewrite the
problem in terms of addition.
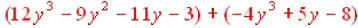(Be sure to change the sign of each term
in the second polynomial). Now this example is similar to example 1. I’ll use the
vertical format: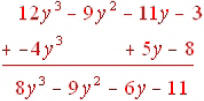 . Notice that there is a space in the second
polynomial under the 9y ² That is because the second polynomial didn’t have a term that
was like 9y ²