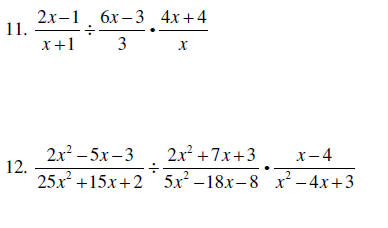Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Multiplying and Dividing Rational Expressions

Multiplying and dividing rational expressions follows the same format as multiplying and
dividing fractions, the only difference is that you must factor the rational expressions
before simplifying the common factors.

Multiplication

You multiply fractions by multiplying across: 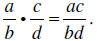If possible, you can simplify
before multiplying – remember you must simplify in both the numerator and
denominator. For example:

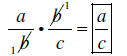
Example 1: Multiply the rational expressions, be sure the answer is simplified:

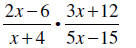
Solution: The first step is to factor everything completely, then get rid of the common
factors between the numerator and denominator.

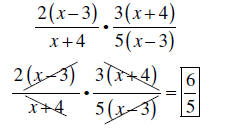
Example 2: Multiply the rational expressions, be sure the answer is simplified:

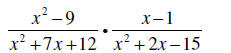
Solution:

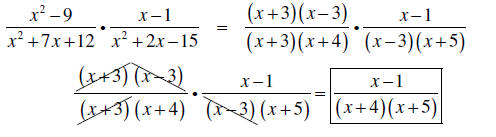
Note: It is easiest (and best) to leave the answer in factored form – it is not necessary to
multiply out the denominator.

Division
Division of fractions is the same as multiplying the first fraction by the reciprocal of the
second fraction (always take the reciprocal of the fraction to the right of the division
symbol).

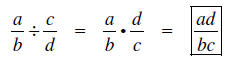
Example 3: Divide – be sure the answer is simplified:

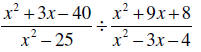
Solution: The first step is to change the division problem to a multiplication problem.
The next step is to factor everything and multiply.

This section heavily depends on your factoring ability. Be sure to review your factoring
worksheets, including how to factor the difference of squares and the sum/difference of
cubes.

Practice Problems

Multiply and divide the rational expressions – be sure all answers are simplified
completely.

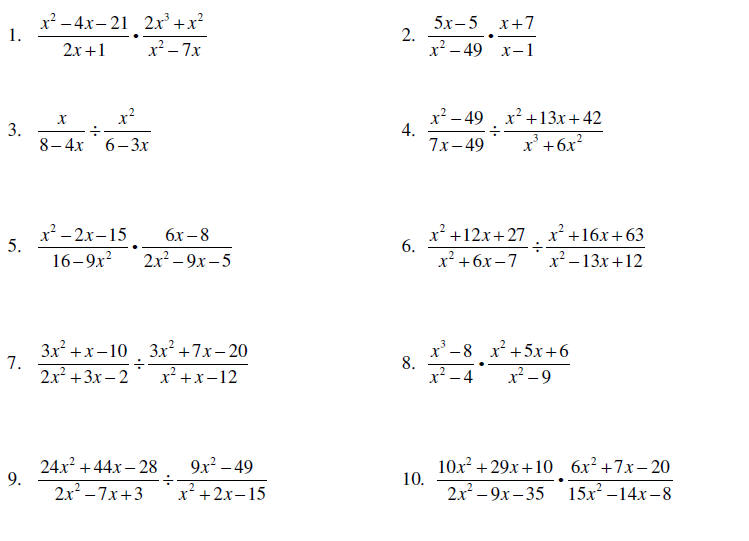
Remember order of operations for the last two problems: