Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Math 1111 Practice Exam for Exam 2

Print Your Name:

(1) No calculator with a CAS on it such as the TI-85 or TI-92.
(2) In some problems you will need to circle more than one alternatives.
(3) Some problems are not multiple choice.

1. Let f(x) = 2x - 1 and g(x) = x² + 1. Find (f ◦ g)(1)

A) 1
B) 2
C) 3
D) 4
E) None of these

2. Let f(x) = 2x - 1 and g(x) = x² + 1. Find (f ◦ f)(1)

A) 1
B) 2
C) 3
D) 4
E) None of these

3. Let f(x) = 2x - 1. Find f^-1(3).

A) 1
B) 2
C) 3
D) 4
E) None of these

4. Find the inverse function of f(x) = 3x - 1.

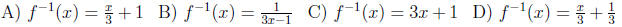E) None of
these.

5. Find the midpoint of (1, 6) and (3, -2).

A) (2, 2)
B) (2, 4)

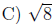
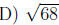
E) None of these

6. Find the distance between (1, 6) and (3, -2).

A) (2, 2)
B) (2, 4)

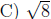
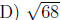
E) None of these

7. Find the center of the circle x² + y² - 2x + 4y - 4 = 0

A) (1, 2)
B) (1,-2)
C) (-1, 2)
D) (-1,-2)
E) None of these.

8. Find the radius of the circle x² + y² - 2x + 4y - 4 = 0

A) 1
B) 2
C) 3
D) 4
E) None of these.

9. Find an equation of the circle centered at (1, 2) with radius 4.

A) x² + y² - 2x - 4y - 11 = 0
B) x² + y² + 2x + 4y - 11 = 0
C) x² + y² - x - 2y - 11 = 0
D) x² + y² + x + 2y - 11 = 0
E) None of these

10. Find the axis of symmetry of the quadratic function y = 2x² - 6x + 3.

A) x = 2
B) y = 2
C) x = 3
D) x = -3
E) y = -3

11. Find the minimum of the quadratic function y = 2x² - 6x + 3.

A) -1.5
B) -0.5
C) 0.5
D) 1.5
E) None of these.

12. Find the vertex of the quadratic function y = 2x² - 6x + 3.

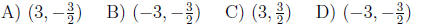E) None of these.

13. Find the range of the quadratic function y = 2x² - 6x + 3.

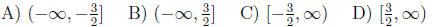E) None of these

14. Find all the zeros of the polynomial function f(x) = x³ + 2x² - 4x - 8.

A) 2
B) 4
C) -2
D) -4
E) 0

15. What is the remainder when x³ + 2x + 1 is divided by x - 1?

A) x² + x + 2
B) x² + x + 3
C) x² - x + 1
D) 4
E) None of these.

16. What is the quotient when x³ + 2x + 1 is divided by x - 1?

A) x² + x + 2
B) x² + x + 3
C) x² - x + 1
D) 4
E) None of these.

17. Simplify (2 + i)(3 - 2i).

A) 8 - i
B) 8 + i
C) 5 - i
D) 5 + i
E) None of these.

18. Add (2 + i) + (3 - 2i).

A) 8 - i
B) 8 + i
C) 5 - i
D) 5 + i
E) None of these.

19. Simplify

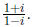
A) 1
B) i
C) 2
D) 2i
E) None of these.

In problems 21, 21, and 22, show your work.

20. Show that f(x) = x³ - 2x - 1 has at least one zero between 1 and 2.

21. Use the long division to find the quotient and remainder when x³ - 3x² + 3x + 4 is
divided by -x + 1.

Quotient =
Remainder =

22. Use the synthetic division to find the quotient and remainder when x³ -3x² +3x+4 is
divided by x - 1.

Quotient =
Remainder =