Math 111 Practice Final
DISCLAIMER. This collection of practice problems is
not guaranteed to be identical, in
length or content, to the actual exam. You may expect to see problems on the
test that are not
exactly like problems you have seen before.
On the actual exam you will have more room to work the problems. You will see
directions
similar to these:
1. Please read directions carefully. Raise your hand if you are not sure what a
problem is asking.
2. You must explain your steps thoroughly and unambiguously to receive full
credit.
3. No calculators or notes are allowed on this exam.
4. You have 50 minutes to complete your test, unless announced otherwise. Do not
spend too
long on any one problem. You do not have to do the problems in order. Do the
easy ones
first. Do not attempt the bonus question until you have completed the rest of the
test. Before
turning in your test, please make sure you have answered and double-checked all
the questions.
5. If you need scratch paper, please raise your hand. You may not use your own
paper. When
you have finished your exam, please turn in any scratch paper you use.
6. Write your solutions in the space provided for each problem, or provide specific instructions
as to where your work is to be found. Make it clear what you want and don't want
graded.
7. Don't stress! I'm rooting for you!
This test is comprehensive. Review all terms, notations, and types of proofs in
chapters 0-9. In
particular, make sure to understand
•Communicating mathematics properly (chapter 0)
•Sets, including sets of numbers and their notations, subsets, set operations
(union, inter-
section, difference, complement, product), and their notations and fundamental
properties,
Venn diagram, partitions (chapter 1, section 4.5)
•Propositions, propositional functions, logical operations (and, or, not,
implication, bicon-
ditional) and their notations, truth tables, tautologies, contradictions,
logical equivalence
and its fundamental properties, quantifiers (universal and existential) (chapter
2)
•Types of proofs: trivial, vacuous, by cases, direct, by contrapositive, by
contradiction
(chapters 3-5)
•Definitions and properties of divisibility and congruences (sections 4.1-4.2)
•Various proof techniques for statements involving: sets, integers,
rational/irrational numbers, positive/negative numbers, any real numbers, absolute value (chapters 4-5)
•Proof of the irrationality of
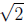(section 5.5)
•Testing, proving and disproving (quantified) statements (including: when an
example/
counterexample is sufficient? When a general proof is required?) (chapter 6)
•Relations and their properties (reflexive, symmetric, transitive), equivalence
relations,
equivalence classes, partitions (chapter 7)
•Functions and their properties (injective, surjective, bijective), composition
of functions
(chapter 8)
•Principle of Mathematical Induction (chapter 9)
1. Prove or disprove the following statement:
Let A, B, and C be sets. Then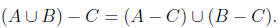
2. Determine whether the compound propositions
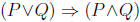and P<=>Q are
logically
equivalent.
3. Let n∈ Z. Prove that if 3n2+ 4n + 2 is even, then n is even.
4. Prove or disprove the following statement:
For any a∈ Z, the number a3 + a + 100 is positive.
5. Consider the relation R dened on Z by aRb iff ab≤0. Determine whether R is
(a) reflexive
(b) symmetric
(c) transitive
(d) an equivalence relation.
6. Consider the function f:Z -> Z defined by
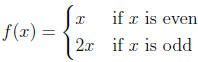
Determine whether f is
(a) one-to-one
(b) onto
(c) bijective.
7. Prove that the number 111 cannot be written as the sum of four integers, two
of which
are even and two of which are odd.
8. Prove that 7 | (32n - 2n) for every nonnegative integer n.
Some kind of BONUS.
Possible question: Give an example of a bijective function f : Z ! N and find its
inverse.