Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Intermediate Algebra Class Notes

What you need to do this week (after attending the first class):

A. Look over Class Notes for 01/14/07 and 01/16/07 (online links found in the
right-hand pane of the homepage).

B. Read the following three (3) webpages (online links found in the left-hand
pane of the homepage):

1. Course Syllabus
2. Course Schedule
3. Course Info & Policies (covered by Quiz #01* on Wed., Jan.23rd)

* This first quiz consists of ten multiple-choice and True-False questions. All
subsequent quizzes will cover math problems selectively picked from the most
recent HomeWork exercises, and will be given without any prior notice.

I. Sets -

A. Symbols: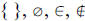
B. Number Sets (p.8) - See Figure 1.2
1. N = {1, 2, 3, ...}
2. W = {0, 1, 2, 3, ...}
3. = {..., -3, -2, -1, 0, 1, 2, 3, ...}
N, W & are all in “roster” notation

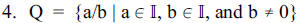
= {x | x is a terminating or a repeating decimal}
5. J = {x | x is a non-terminating, non-repeating decimal}
6. 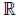= {x | x is a decimal}

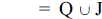
Q, J &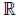 are all in “set-builder” notation

II. Examples (pp.10-12): Exercises #34,68,14,80

HW: Read pp.2-10 (textbook)
pp.10-12 / Exercises #1-97 (every other odd)

I. Absolute Value (p.15):
l x l = distance from zero (on a number line)

II. Opposites:

A. - (-a) = a
B. a – (-b) = a + b

III. Division involving Zero:

A. 0 ÷ a = 0
e.g., 0 ÷ 7 = 0 (since 0 = 7 × 0)
B. a ÷ 0 is “undefined”
e.g., 7 ÷ 0 = ? (requires 7 = 0 × ?)
note: no such number exists, i.e., undefined

IV. Distributive Property (pp.21-22):

a(b ± c) = ab ± ac

V. Examples (pp.24-25): Exercises #8,46,90,100,
122

HW: Read pp.13-24 (textbook)
pp.24-26 / Exercises #1-141 (every other odd)