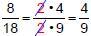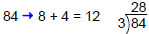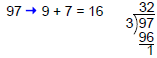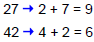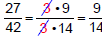Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Simplifying Fractions

To simplify a fraction means to write the fraction in simplest form. A
fraction is "simplified" when the numerator and denominator have
no common factors other than1.

Consider the following fractions. Can they be simplified?

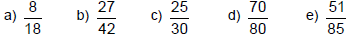
To see if they can, we use divisibility rules and prime factorization to
factor the numerator and denominator. Then we cancel common factors.

Divisibility Rule for 2

Rule for 2

Divisibility rules are based on patterns of
multiplication.

When we list the multiples of 2,we
get even numbers, numbers that end
in 2,4,6,8 or 0:

Multiples of 2: 2, 4, 6, 8, 10, ...

This means all even numbers can be
divided by 2.

Example 1: Simplify

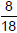The numerator and denominator are
even numbers.

To simplify the fraction, divide each
number by 2 and cancel the common
factor of 2:

Divisibility Rule for 3

Rule for 3

If a number's digits add to a multiple
of 3,the number can be divided by 3.
For example,

84 is divisible by 3 because its
digits add to a multiple of 3:

97 is not divisible by 3 because its
digits don't add to a multiple of 3:

Example 2: Simplify

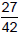The numerator and denominator can
be divided by 3:

To simplify the fraction, divide each
number by 3 and cancel:

Divisibility Rules for 5 and 10

Rule for 5

If a number ends in 0 or 5,divide the
number by 5.

Multiples of 5: 5, 10, 15, 20, …

Rule for 10

If the number ends in 0, divide by 10.

Multiples of 10: 10, 20, 30, …

Example 3: Simplify

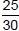Divide each number by 5 and cancel
the common factor: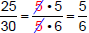

Example 4: Simplify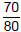

Canceling the 0's,divides each
number by 10: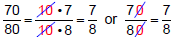

Applying Divisibility Rules

Example5:Can the fraction 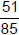be simplified?

Since the numerator,51,can be divided by 3 and the denominator,85,
can be divided by 5,we can apply each rule separately. Notice the
the numbers share a common factor of 17:

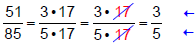	divide 51 by 3
	divide 85 by 5

Practice Exercise 1

Simplify each fraction.

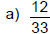
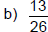
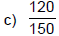
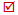Check answers

Solution − Practice Exercise 1

Simplify each fraction.

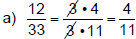
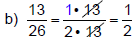	←When the number in the numerator cancels, we must write a"1."
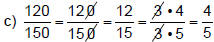	← Cancel the 0's first.

Prime Factorization

A prime number is divisible by itself and1.Prime numbers include,

2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, …

A number that is not prime is called composite because the number
can be written as a product of its prime factors. For example, the
number6 is composite because we can factor 6 and write it as a
product of its prime factors,2 and 3:

6 = 2· 3