Random-Number Generation
Tests for Random Numbers
 Two categories:
Two categories:
 Testing for uniformity:
Testing for uniformity:
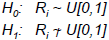
![]() Failure to reject the null hypothesis,
H0, means that
evidence of
Failure to reject the null hypothesis,
H0, means that
evidence of
non-uniformity has not been detected.
 Testing for independence:
Testing for independence:
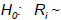 independently
independently
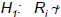 independently
independently
![]() Failure to reject the null hypothesis, H0, means that evidence of
Failure to reject the null hypothesis, H0, means that evidence of
dependence has not been detected.
 Level of significance α, the probability of rejecting H0 when it
Level of significance α, the probability of rejecting H0 when it
is true:
α = P(reject H0|H0 is true)
 When to use these tests:
When to use these tests:
 If a well-known simulation languages or random-number
If a well-known simulation languages or random-number
generators is used, it is probably unnecessary to test
 If the generator is not explicitly known or documented, e.g.,
If the generator is not explicitly known or documented, e.g.,
spreadsheet programs, symbolic/numerical calculators, tests
should be applied to many sample numbers.
 Types of tests:
Types of tests:
 Theoretical tests: evaluate the choices of m, a, and c without
Theoretical tests: evaluate the choices of m, a, and c without
actually generating any numbers
 Empirical tests: applied to actual sequences of numbers
Empirical tests: applied to actual sequences of numbers
produced. Our emphasis.
Frequency Tests
![]() [Tests for RN]
[Tests for RN]
 Test of uniformity
Test of uniformity
 Two different methods:
Two different methods:
 Kolmogorov-Smirnov test
Kolmogorov-Smirnov test
 Chi-square test
Chi-square test
Kolmogorov-Smirnov Test
![]() [Frequency Test]
[Frequency Test]
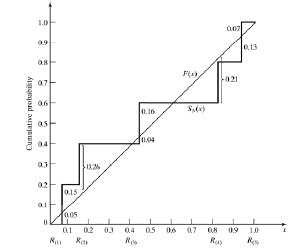
 Compares the continuous cdf, F(x), of the uniform
Compares the continuous cdf, F(x), of the uniform
distribution with the empirical cdf, SN(x), of the N sample
observations.
 We know: F(x) = x, 0 ≤ x ≤1
We know: F(x) = x, 0 ≤ x ≤1
 If the sample from the RN generator is
If the sample from the RN generator is
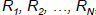 , then the
, then the
empirical cdf, SN(x) is:
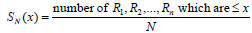
 Based on the statistic: D = max| F(x) - SN(x)|
Based on the statistic: D = max| F(x) - SN(x)|
 Sampling distribution of D is known (a function of N, tabulated in
Sampling distribution of D is known (a function of N, tabulated in
Table A.8.)
 A more powerful test, recommended.
A more powerful test, recommended.
 Example: Suppose 5 generated numbers are 0.44, 0.81, 0.14,
Example: Suppose 5 generated numbers are 0.44, 0.81, 0.14,
0.05, 0.93.
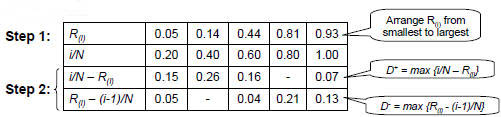
Step 3: 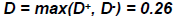 Step 4: For α = 0.05, 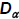 = 0.565 > D = 0.565 > DHence, H0 is not rejected. |
 |
Chi-square test
![]() [Frequency Test]
[Frequency Test]
 Chi-square test uses the sample statistic:
Chi-square test uses the sample statistic:
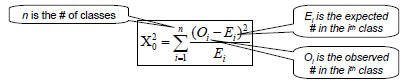
 Approximately the chi-square distribution with n-1
degrees of
Approximately the chi-square distribution with n-1
degrees of
freedom (where the critical values are tabulated in Table A.6)
 For the uniform distribution, Ei, the expected number in the each
For the uniform distribution, Ei, the expected number in the each
class is:
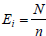 ,where N is the total
# of observation
,where N is the total
# of observation
 Valid only for large samples, e.g. N >= 50
Valid only for large samples, e.g. N >= 50
Tests for Autocorrelation
![]() [Tests for RN]
[Tests for RN]
 Testing the autocorrelation between every m numbers
Testing the autocorrelation between every m numbers
(m is a.k.a. the lag)
 The autocorrelation
The autocorrelation
 between numbers:
between numbers: 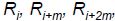
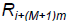
 M is the largest integer such that i +(M
+1)m ≤ N
M is the largest integer such that i +(M
+1)m ≤ N
 Hypothesis:
Hypothesis:
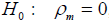 if numbers are independent
if numbers are independent
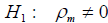 , if numbers are dependent
, if numbers are dependent
If the values are uncorrelated:
 For large values of M, the distribution of the estimator
of
For large values of M, the distribution of the estimator
of 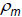 ,
,
denoted 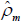 is approximately normal.
is approximately normal.
 Test statistics is:
Test statistics is:
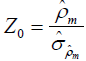
 Z0 is distributed normally with mean = 0 and variance =
1
Z0 is distributed normally with mean = 0 and variance =
1
 If
If 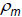 > 0, the subsequence has positive autocorrelation
> 0, the subsequence has positive autocorrelation
 High random numbers tend to be followed by high ones, and vice versa.
High random numbers tend to be followed by high ones, and vice versa.
 If
If 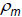 < 0, the subsequence has negative autocorrelation
< 0, the subsequence has negative autocorrelation
 Low random numbers tend to be followed by high ones, and vice versa.
Low random numbers tend to be followed by high ones, and vice versa.
Shortcomings
![]() [Test for Autocorrelation]
[Test for Autocorrelation]
 The test is not very sensitive for small values of M,
The test is not very sensitive for small values of M,
particularly when the numbers being tests are on the low
side.
 Problem when “fishing” for autocorrelation by performing
Problem when “fishing” for autocorrelation by performing
numerous tests:
 If α = 0.05, there is a probability of 0.05 of rejecting a true
If α = 0.05, there is a probability of 0.05 of rejecting a true
hypothesis.
 If 10 independence sequences are examined,
If 10 independence sequences are examined,
![]() The probability of finding no significant autocorrelation, by
The probability of finding no significant autocorrelation, by
chance alone, is 0.9510 = 0.60.
![]() Hence, the probability of detecting significant autocorrelation
Hence, the probability of detecting significant autocorrelation
when it does not exist = 40%


