Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Equation of a Line

1 Equation of a Line 3.4

By the end of this section, you should be able to solve the following problems.

1. Find the equation of the line with the given slope and passing through
the given point.

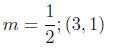
2. Rewrite the equation in slope-intercept form.

3x − 5y = 4

3. Find the equation of the line passing through the given points in standard
form.

(−2,−3), (1, 2)

4. Find the equation of the line passing through the given points, in standard
form.

(−2,−3) and (1, 2)

2 Concepts

There are three forms of the equation of a line. The most general form is
called standard form. The standard form of an equation of a line is given
below.
Ax + By = C

In the above equation, the coefficient of x can be positive, or zero. Whenever
the coefficient of x is negative, multiply both sides of the equation by -1
to make it positive. The coefficient of y can be positive, negative, or zero. A
line will exist so long as A and B are not both zero at the same time. The
second form of the equation of a line is called the point-slope form of the
equation of a line, and it is given below:

y − y₁ = m(x − x₁)

In the equation above, m stands for the slope and (x₁, y₁) designate a
point. The third equation is called the slope-intercept form of the equation
and it is given below.

y = mx + b

In the above equation m stands for the slope and b is the y-intercept. In
our first example, we build the equation of a line using a point and a slope.

2.1 Example

Find the equation of a line with the given slope and passing through a given
point.

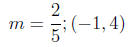
Since we are given a point and a slope, we substitute into the point-slope
form of the equation of a line.

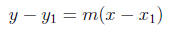
Substituting (-1,4) for x₁ and y₁:

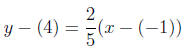
Simplifying:

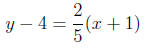
Multiplying both side of the equation by 5 to eliminate denominators.

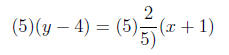
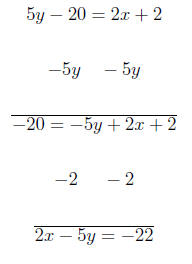
In our next example we rewrite an equation in slope-intercept form.

2.2 Example

Rewrite the following equation in slope intercept form.

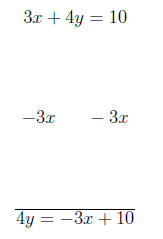
Dividing both sides by 4 we have:

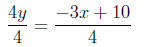
Distributing the denominator we have:

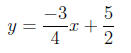
In our last example, we construct a line using two points.

2.3 Example

Find the equation of a line that passes through the following points, and
write it in standard form.

(−1, 5) and (2, 1)

First we find the slope of the line.

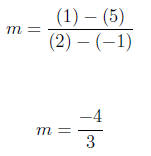
Substituting into the point-slope equation we have.

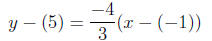
Simplifying:

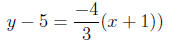
Multiplying both sides by 3:

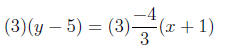
Clearing fractions gives:

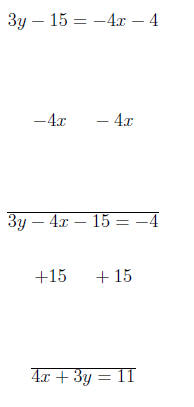
3 Facts

1. Than standard form of the equation of a line is:
Ax + By = C
2. The point-slope form of the equation of a line is:
y − y₁ = m(x − x₁)
3. The slope-intercept from of the equation of a line is:
y = mx + b

4 Exercises

1. Find the equation of the line with the given slope and passing through
the given point.

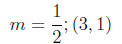
2. Rewrite the equation in slope-intercept form.

3x − 5y = 4

3. Find the equation of the line passing through the given points, in standard
form.
(−1, 2) and (2, 3)

4. Find the equation of the line passing through the given points, in standard
form.
(−2,−3) and (1, 2)

5 Solutions

1. Find the equation of the line with the given slope and passing through
the given point.

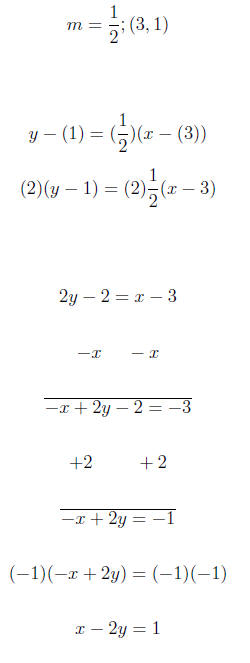
2. Rewrite the equation in slope-intercept form.

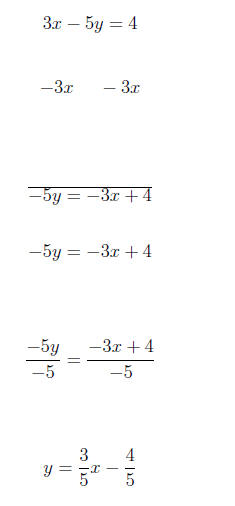
3. Find the equation of the line passing through the given points, in standard
form.

(−1, 2) and (2, 3)

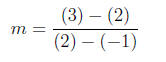
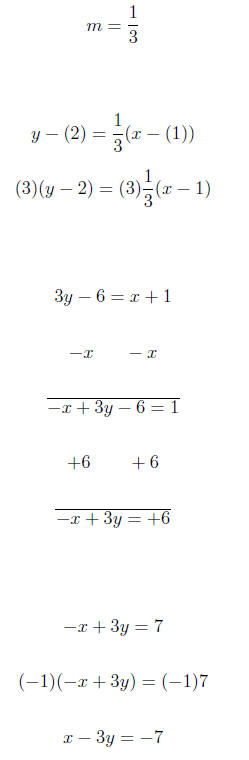
4. Find the equation of the line passing through the given points, in standard
form.

(−2,−3) and (1, 2)

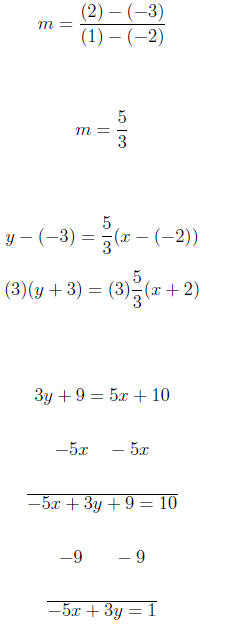
−5x + 3y = 1
(−1)(−5x + 3y) = (−1)1
5x − 3y = −1