Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Intermediate Algebra Worksheet

1. One often needs to multiply polynomials in problems involving areas and volumes.

(a) The length of a rectangular field is 10 meters more than twice the width. Let w be the width.
What is the area of the field?

(b) A triangular roof panel has a height half as long as its base. If the base has length b, what is the
area of the roof panel.

(c) A rectangular block has a width 5 meters shorter than three times its length. The height is 3
times the length. If the width of the block is w, what is its volume?

(d) A silo is in the shape of a cylinder with a hemispherical top. The radius of the silo is one third of
its height. If the height is h, find the volume of the silo.

2. Bill Gates goes insane and offers you that on the first day of the month he will give you 1 dollar, on the
second day f dollars, and the third day f² dollars, on the fourth day f³ dollars, and so on, increasing
by a factor of f every day until the end of the month.

(a) The amount of money you have collected after d days is given by the formula

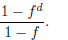(1)

Verify that this formula works after 2 days, 4 days, and 6 days using f = 2, i.e. assuming that
the amount he gives you doubles every day.

(b) Use synthetic division to rewrite the formula for d = 4 days. Check that your result agrees with
your answer to part (a) for f = 2.

3. A box has a length 10 cm less than twice its width. If the width is w cm and the volume of the box is
2w³ − 20w² + 50w cm³, then:

(a) Use synthetic division to find the height of the box in terms of w.

(b) What is the area of the base of the box?

(d) Find the the volume of a box whose with the same length and width, but twice the height.