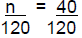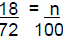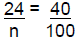Solving Percent Problems
| Area/Skill Mathematics Language Arts, Reading Language Arts, Writing |
Cognitive Skill Level Comprehension, Application, Analysis, Synthesis |
Submitted by Monica Watson |
Location Southwest MS Community College |
| Goal/Objective: Students will comprehend and analyze what differentiates the part and the whole in percent problems Lesson Outline: Math: Determine the part and whole to set up a proportion to solve percent problems. Language Arts, Reading: Use the Internet to find and read biographical essays or comments on mathematicians. Language Arts, Writing: Demonstrate proficiency in holistic writing practices. Introduction: This lesson provides a step by step approach to solving problems with unknowns, thus an intro for solving linear equations with one variable. Students will use cognitive skill levels to classify, arrange, solve, research, decipher, and compare unknown quantities and actual savings versus proposed savings. Students will also utilize the logical/mathematical and linguistic learning styles. Activity: Refer to handout information sheet. 1) Discuss the three types of questions in percent problems. Explain to students how to differentiate between the part and whole of a percent problem and use a proportion to solve for the missing number. 2) Have students use the graphic organize to brainstorm what they think they know about percents and then write a journal writing describing the steps taken to solve for the missing number in one of the types of percent problems. 3) Have students utilize the Internet or periodicals to search for biographies on mathematicians. Also have students search for advertisements indicating percentage discounts on similar name brand products and survey any proposed savings. Debriefing/Evaluation Activity: Ask students to discuss any difficulties in determining the part and the whole. Ask students to draw charts or explain the process of substituting the known values into the correct position when setting up a proportion. |
Materials/Texts/Realia/Handouts Newspaper Sales Advertisements Graphic Organizer Articles from the Internet Extension Activity ESE Accommodations
|
||
| Real-Life Connection: Since adults are also consumers, the lesson’s reference to real-life consumer practices will address how viable it will be to understand how percentages are derived and demonstrated comparison techniques regarding advertised discounted prices. Percents are commonly used in many of the adult learners’ livelihood such as calculating percents for interest on various types of loans, discounts and taxes. |
|||

Solving Percent Problems
A percent problem can be solved by setting up a proportion that shows that the
relationship
between the part and the whole is the same as the relationship of a percent part
to 100%.

proportion occurs when two ratios are equal to each other.
The proportion below can be
stated as: “a is to b as c is to d.” This also can be written in the fractional
form as:
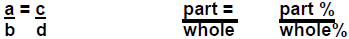
| Example 1) What is 40% of 120? You are looking
for the part of 120. Set up the proportion:
Example 2) 18 is what percent of 72? You are
looking for the percent part.
Example 3) 24 is 40% of what number? You are
looking for the whole.
|
Solving Percent Problems
Use the proportion sample to set up a percent problem. To solve a percent
problem you must
first:
% Read the problem carefully
% Next decide if the number you are looking for is the part, the whole,
or the percent part.
% The percent whole is always 100%.
% Often, to find the whole or the percent part, it is usually most reliable to
use a proportion
to solve the problem.