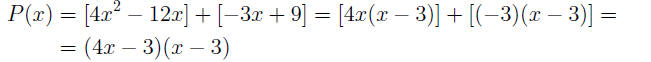FACTORING POLYNOMIALS

To factor a polynomial means to write it a product of polynomials.
EXAMPLE: 4x² − 15x + 9 = (4x − 3)(x − 3). The method, by which this
factoring was obtained, will be explained below (see method D).
TIP: Whenever you want to factor a polynomial, try the four methods ex-
plained below, in the order A, B, C, D (if applicable)

A: Pulling out obvious factors.

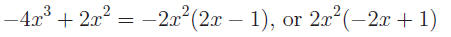
B: Recognize one of the Special Products. These are:
• Difference of Squares: A² − B² = (A + B)(A − B);
• Square of a Sum: A² + 2AB + B2² = (A + B)²;
• Square of a Difference: A² − 2AB + B² = (A − B)²;
• Difference of Cubes: A³ − B³ = (A − B)(A² + AB + B²);
• Sum of Cubes: A³ + B³ = (A + B)(A² − AB + B²).

For instance,

• to factor 4x^2 − 25, we use the Difference of Squares, with A = 2x and
B = 5:

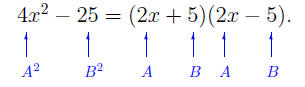
• to factor 9y^2 −30y +25, we use the Square of a Difference, with A = 3y
and B = 5:

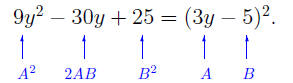
• to factor 125z^3 + 8, we use the Sum of Cubes, with A = 5z and B = 2:

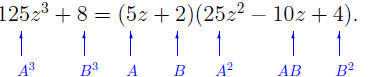
C: Grouping
1. Split into (smaller) groups, which all share a common factor.
2. Pull that factor out.

For instance, to factor P(x) = x^3 + x^2 − 2x − 2, we form two groups (using
square brackets), we factor them (separately), and finally we pull the (x+1)
factor out:

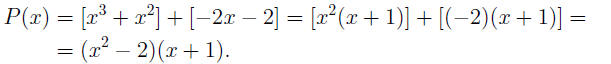
D: Split-Group Factoring of Quadratic Trinomials. This refers to
polynomials of the form

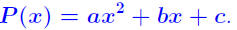
The method (”the p & q Game”) involves the following steps:
1. Find numbers p and q, such that p · q = a · c and p + q = b
2. Split the polynomial into two groups: P(x) = [ax^2 + px] + [qx + c].
3. Factor by grouping (see method C). The two groups will always have a
common factor!

For instance, suppose we want to factor:

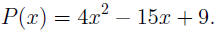
(The coefficients are: a = 4, b = −15, and c = 9.)

We start off by looking for numbers p and q, such that p · q = 4 · 9 = 36
and p + q = −15. One working combination is: p = −12 and q = −3.
Then we split and factor by grouping: