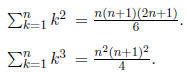Try the Free Math Solver or Scroll down to Resources!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Sequences and Sums

A sequence is a function t from a subset of the integers (usually N or Z+) to a set S. In this
discussion, the set S will be a set of numbers but we could have a sequence of colors, musical notes,
or even computer programs.

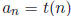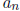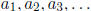We often write . Each is a term of the sequence. The sequence may
be denoted by 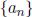or 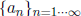. The numbers, 1, 2, 3,... are the term indices and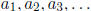
are the term values

1 Sequence Examples

Can you give the next term of each of these sequences? Can you give the function t(n) that defines
the sequence? Assume the first term is .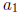

2 Some Special Sequences

2.1 Arithmetic Sequences

An arithmetic sequence is a sequence in which each term equals the preceding term plus a constant.
A general arithmetic sequence looks like this a, a + d, a + 2d, a + 3d,... The first term is a and the
constant difference between terms is d.
What is the n^th term of the sequence a, a + d, a + 2d, a + 3d, : : :?
What is the next term and the nth term of each of these sequences?

4, 7, 10, 13, 16, 19, ...
-7,-1, 5, 11, 17, 23, ...

2.2 Geometric Sequences

A geometric sequence is a sequence in which each term equals the preceding term times a constant.
A general geometric sequence looks like this a, ar, ar2, ar3, ar4,... the first term is a and the
constant ratio between successive terms is r.
What is the n^th term of the sequence a, ar, ar², ar³, ar⁴,...?
What is the next term and the nth term of each of these sequences?

2, 6, 18, 54, 162, ...
1,-4, 16,-64, 256,...

2.3 Quadratic Sequences

A quadratic sequence is a sequence whose n^th term is given by a quadratic function, .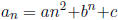
Here are some quadratic sequences. Can you find the quadratic function that generates them?

1, 4, 9, 16, 25, 36, ...
6, 15, 28, 45, 66, 91,...

An arithmetic sequence is given by a linear function and the difference between successive terms is
a constant. In a quadratic sequence the differences between successive terms are given by a linear
function and the second differences are constant. For example:

sequence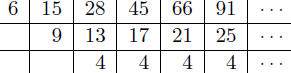
differences
second differences

3 Series and Partial Sums

A series is a sum of the terms of a sequence. Since a sequence has infinitely many terms, a series
is the sum of infinitely many terms. We often sum only the first n terms of a sequence. The sum
of the first n terms is called the nth partial sum. The following is a sum of an infinite number of
terms.

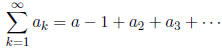
Below is the sum of the first n terms. This is the n^th partial sum. k is the index of summation, 1
is the lower limit, n is the upper limit.

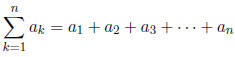
This is also a partial sum. j is the index of summation, m is the lower limit, n is the upper limit.

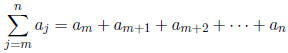
3.1 Arithmetic Sums

An arithmetic sum is a sum of terms of an arithmetic sequence

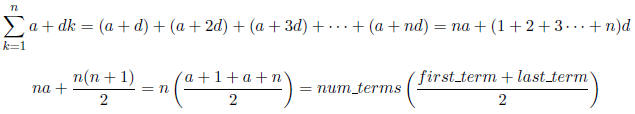
3.1.1 Examples

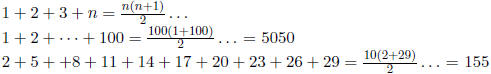
3.2 Geometric Sums and Series

A geometric sum is a sum of terms of a geometric sequence.

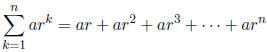
or, summing from 0

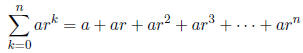
With geometric sequences, summing the infinite sequence may be meaningful. infinite sums are
called series.

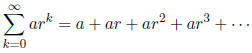
Let's find a formula fort the nth partial sum

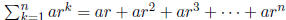
Let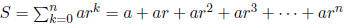
Then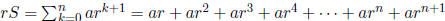

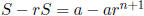as all the other terms cancel out when we subtract rS from S.

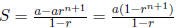
3.2.1 Examples

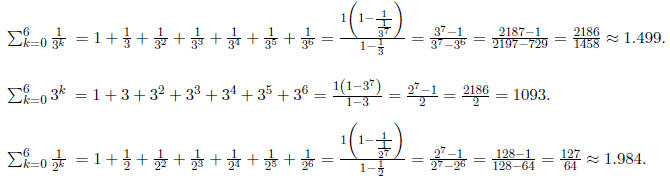
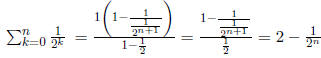.What happens when n gets very large?

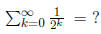
3.3 Some Special Sums